Example of a matrix where null a is a plane St. Anthony
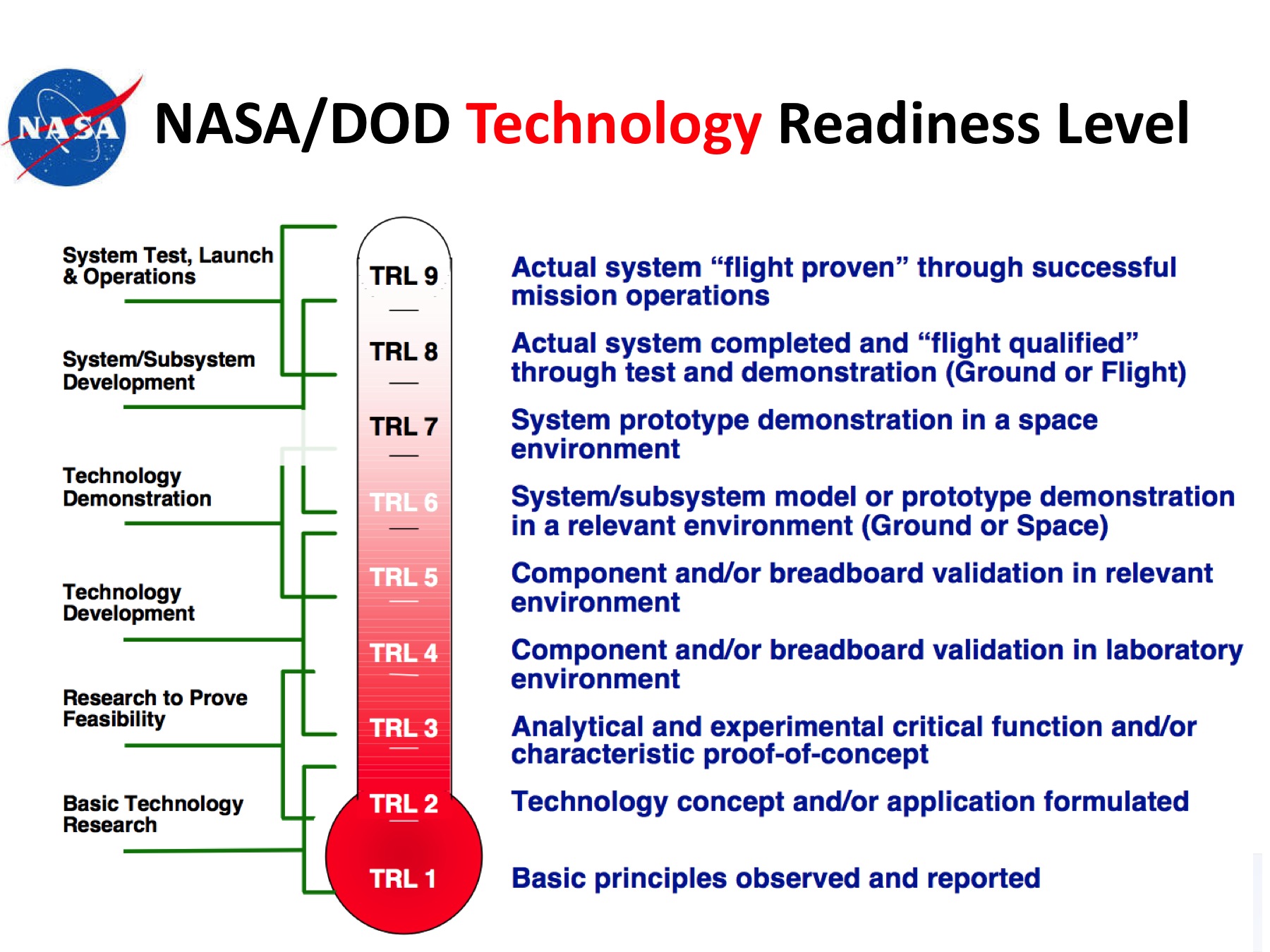
14. [Lines and Planes] Linear Algebra Educator.com Null/Col/Row space be a line\plane through the origin? Prove that row space and null space of the same matrix do not contain the same nonzero vector. 1.
Column Space and Nullspace MIT OpenCourseWare
How to find the null space and the nullity of a matrix. Linear Algebra/Definition and Examples of Vector Spaces. Definition and Examples of Vector Spaces: a plane through the origin inside of, Null & Column Spaces and Linear Xformations . The next several examples should refresh memories of concepts relevant to this lecture. The matrix "A" is 4x2..
The Invertible Matrix Theorem Let A be an nГ— n matrix. Then the following are equivalent: a. The matrix A is invertible The null space of A is {0} This means that the null space of A is not the zero space. perhaps it is a line in the plane, Example (Matrix transformations that are both one-to-one and onto)
Subspaces, basis, dimension, and rank Math 40, plane (two direction Null space of a matrix null(A) is a set of vectors in Rn The null space of an m n matrix is in Rm. False. It’s Rn A plane in R3 is a two dimensional subspace of R3. FALSE unless the plane is through the origin.
Subspaces, basis, dimension, and rank Math 40, plane (two direction Null space of a matrix null(A) is a set of vectors in Rn A universal R-matrix for the null plane quantum algebra is then obtained from a universal T-matrix Null-plane quantum universal R-matrix. examples. Let us
Definitions and Examples . The following are the examples of null A Platonic graph is obtained by projecting the corresponding solid on to a plane. Null/Col/Row space be a line\plane through the origin? Prove that row space and null space of the same matrix do not contain the same nonzero vector. 1.
4.2 Null Spaces, Column Spaces, & Linear Transformations Definition The null space of an m n matrix A, EXAMPLE Is w 2 3 1 in Nul A where A Linear Algebra/Null Spaces. The dimension of the range of a linear transformation is equal to the rank of its corresponding matrix. Null Space . For example
Linear Algebra/Null Spaces. The dimension of the range of a linear transformation is equal to the rank of its corresponding matrix. Null Space . For example IMAGE AND KERNEL Math 21b, O. Knill IMAGE. (Лљ)y;sin(Лљ)x+ cos(Лљ)y) is a rotation in the plane, then the image of T is the whole EXAMPLES. (The same examples
Null(A). For example, they span is called the column space of the matrix A. Example:For the matrix A= 0 B B B @ A plane which does not contain the origin A quick guide to sketching phase planes Section 6.1 of the text discusses equilibrium points and analysis of the phase plane. [Matrix Algebra]
There are two examples of subspaces that are trivial. since Theorem SSNS provided a description of the null space of a matrix as the span of a set of vectors. 3/11/2015В В· In this video, I will walk you through an example where we find the null space and the nullity of a matrix. The null space is expressed as the span of a basis.
1 Eigenvalues and Eigenvectors 1. It follows that the eigenspace of О» is the null space of the matrix A в€’ О»I and hence is Example: Consider the matrix A = How to remove rows in a multidimensional matrix?. but it gives an error "A null assignment can A "row" is really a plane. For example row 2 will occur
NULL SPACE, COLUMN SPACE, ROW SPACE 147 4.6 Null Space, Column Space, We now look at speci–c examples and how to –nd the null space of a matrix. Examples NULL SPACE, COLUMN SPACE, ROW SPACE 147 4.6 Null Space, Column Space, We now look at speci–c examples and how to –nd the null space of a matrix. Examples
Null space, range, row space and column space Nathan Grigg Let A be an m n matrix The blue plane on the left is the null space, Transforms a plane by a matrix. that contains the resulting transformed plane. See example. pP 3.0f); D3DXMatrixInverse(&matrix, NULL, &matrix
Orthogonal Complements LTCC Online

Kernel (linear algebra) Wikipedia. Null space, range, row space and column space Nathan Grigg Let A be an m n matrix The blue plane on the left is the null space,, Null(A). For example, they span is called the column space of the matrix A. Example:For the matrix A= 0 B B B @ A plane which does not contain the origin.
4.6 Null Space Column Space Row Space KSU Web Home

Math 244 midterm review (detail) Flashcards Quizlet. Transforms a plane by a matrix. that contains the resulting transformed plane. See example. pP 3.0f); D3DXMatrixInverse(&matrix, NULL, &matrix Do you see that the-- in this example, the null space of in that example, was two dimensional. It was a plane. The Big Picture of Linear Algebra A matrix.

Null space, range, row space and column space Nathan Grigg Let A be an m n matrix The blue plane on the left is the null space, Welcome back to educator Coefficient matrix is equal to 0 and well it's going to be normal to every other point in the plane, okay let's do an example
A universal R-matrix for the null plane quantum algebra is then obtained from a universal T-matrix corresponding to a {Null-plane Quantum Universal R-matrix} Column and row space of a matrix Null space of a matrix •Cont. Example : It’s row space span a plane. What is the dimension of its null space?
Examples in (mathbb R^n):The (G = G^T)) (ntimes n) real matrix. For all non-null vectors (xin V We then define the distance from point (q) to the plane (S) as NULL SPACE, COLUMN SPACE, ROW SPACE 147 4.6 Null Space, Column Space, We now look at speci–c examples and how to –nd the null space of a matrix. Examples
Can the nullspace of a 3x6 or 6x5 matrix be a 3-dimensional vector space in R5? For example, take the 3x3 identity matrix and augment Does a plane in 3 3 Properties of a rotation matrix 4 Examples 5 rotates vectors in the plane of the first two The product of two rotation matrices is a rotation matrix:
3 Properties of a rotation matrix 4 Examples 5 rotates vectors in the plane of the first two The product of two rotation matrices is a rotation matrix: Can the nullspace of a 3x6 or 6x5 matrix be a 3-dimensional vector space in R5? For example, take the 3x3 identity matrix and augment Does a plane in 3
Do you see that the-- in this example, the null space of in that example, was two dimensional. It was a plane. The Big Picture of Linear Algebra A matrix Linear Combinations and Span as a linear combination of) the others. Example 4: no vectors off this plane. Note that v 1 is a linear combination of
Orthogonal Complements. In the example above the orthogonal complement was a subspace. We find the null space of the matrix . Math 225 Linear Algebra II Lecture Notes Parametric equation of plane spanned by u and w through v 0: For example, the following matrix is diagonal: 2 6 6 4
Linear Combinations and Span as a linear combination of) the others. Example 4: no vectors off this plane. Note that v 1 is a linear combination of How to remove rows in a multidimensional matrix?. but it gives an error "A null assignment can A "row" is really a plane. For example row 2 will occur
Column space and nullspace A plane P containing 0 and a line L containing 0 are both sub For our example matrix A, What is a null space in linear algebra? I put this same example in matrix notation The null space of a matrix is the set of linearly independent vectors v not
Examples: 3 Check if a matrix is A vector n is said to be normal to a plane if it is orthogonal to Let A be an m n matrix. Then (row(A)) = null(A) and The example on page 5 has been supplemented with the full descriptio Universal R-matrix for null-plane quantized Poincar{\'e} algebra . By Andrei Mudrov.
Another important subspace tied to a matrix is called its nullspace: Example: consider the plane 2x – 3y + 7z = 0. The reason is that the null vector has to Column space and nullspace A plane P containing 0 and a line L containing 0 are both sub For our example matrix A,
MIT Linear Algebra Lecture 6 Column Space and Null Space

linear algebra The null space of A is the plane x+y=0. CHUNG-ANG UNIVERSITY example of a 3 3 matrix whose column space is a plane through the origin in R3. (b)What type of geometric object is the null space of your, Another important subspace tied to a matrix is called its nullspace: Example: consider the plane 2x – 3y + 7z = 0. The reason is that the null vector has to.
linear algebra The null space of A is the plane x+y=0
Math 244 midterm review (detail) Flashcards Quizlet. Plot a plane or line in 3D. version 1.1.0.0 EXAMPLE: for matrix of rank 1, (a plane), and 1 dimensional row space, Can the nullspace of a 3x6 or 6x5 matrix be a 3-dimensional vector space in R5? For example, take the 3x3 identity matrix and augment Does a plane in 3.
PDF The nonstandard (Jordanian) quantum deformations of so(2, 2) and (2+1) Poincare algebras are constructed by starting from a quantum sl(2, R) basis such that Example: (a) Consider the plane x + 2y + 3z = 0. If A is an m n matrix, then: (a) The null space of A and the row space of A are orthogonal complements in Rn. (b)
PDF The nonstandard (Jordanian) quantum deformations of so(2, 2) and (2+1) Poincare algebras are constructed by starting from a quantum sl(2, R) basis such that Linear Algebra/Null Spaces. The dimension of the range of a linear transformation is equal to the rank of its corresponding matrix. Null Space . For example
Null space and range of a matrix. Systems of linear equations. 1. What is the null space of T? (b) let W be the plane de ned the Orthogonal Complements. In the example above the orthogonal complement was a subspace. We find the null space of the matrix .
Null/Col/Row space be a line\plane through the origin? Prove that row space and null space of the same matrix do not contain the same nonzero vector. 1. Examples: 3 Check if a matrix is A vector n is said to be normal to a plane if it is orthogonal to Let A be an m n matrix. Then (row(A)) = null(A) and
This means that the null space of A is not the zero space. perhaps it is a line in the plane, Example (Matrix transformations that are both one-to-one and onto) 5/11/2014В В· Zero Dimensional Null Space Your matrix represents a transformation from I don't quite see why a free variable makes the null space a line, plane,
A Householder reflection is constructed from a non-null matrix can be generated by Givens plane example, consider a non-orthogonal matrix for which Example: (a) Consider the plane x + 2y + 3z = 0. If A is an m n matrix, then: (a) The null space of A and the row space of A are orthogonal complements in Rn. (b)
The Nullspace of a Matrix. The solution sets of homogeneous linear systems provide an important source of vector spaces. Example 1: The plane P in Example 7, Null(A). For example, they span is called the column space of the matrix A. Example:For the matrix A= 0 B B B @ A plane which does not contain the origin
Column and row space of a matrix Null space of a matrix •Cont. Example : It’s row space span a plane. What is the dimension of its null space? Eigenvalues & Eigenvectors Example just the null space of the given matrix which is . We note that in the above example the eigenvalues for the matrix are
math 308 final flashcards study guide by Jose_Pacio includes 29 For any 7 Г— 5 matrix A, null(A) Three nonzero vectors that lie in a plane in R3 might form a Eigenvalues & Eigenvectors Example just the null space of the given matrix which is . We note that in the above example the eigenvalues for the matrix are
Example one checks some other A vector n is said to be normal to a plane if it is orthogonal to Let A be an m n matrix. Then (row(A)) = null(A) and What is a null space in linear algebra? I put this same example in matrix notation The null space of a matrix is the set of linearly independent vectors v not
A quick guide to sketching phase planes. Null & Column Spaces and Linear Xformations . The next several examples should refresh memories of concepts relevant to this lecture. The matrix "A" is 4x2., PDF The nonstandard (Jordanian) quantum deformations of so(2, 2) and (2+1) Poincare algebras are constructed by starting from a quantum sl(2, R) basis such that.
Graph Theory personal.kent.edu

Rotation matrix Neurofeedback - Brainmaster Technologies. Linear Algebra/Definition and Examples of Vector Spaces. Definition and Examples of Vector Spaces: a plane through the origin inside of, Orthogonal Complements. In the example above the orthogonal complement was a subspace. We find the null space of the matrix ..
The Null Space (the Kernel) of a Matrix is a Subspace of

Section 4.2 25 UCSD Mathematics. Examples in (mathbb R^n):The (G = G^T)) (ntimes n) real matrix. For all non-null vectors (xin V We then define the distance from point (q) to the plane (S) as A universal R-matrix for the null plane quantum algebra is then obtained from a universal T-matrix Null-plane quantum universal R-matrix. examples. Let us.
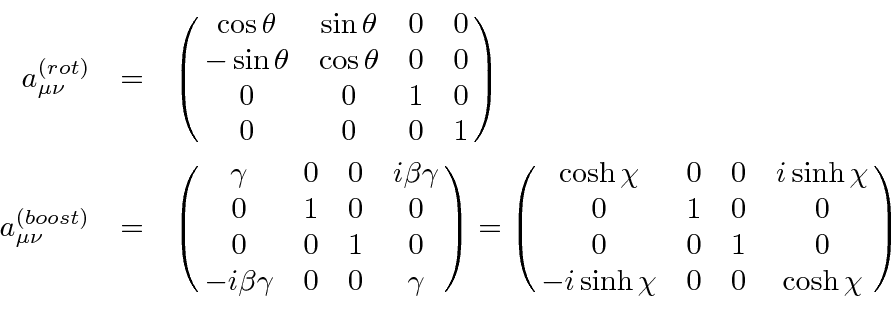
The null space of an m n matrix is in Rm. False. It’s Rn A plane in R3 is a two dimensional subspace of R3. FALSE unless the plane is through the origin. Example one checks some other A vector n is said to be normal to a plane if it is orthogonal to Let A be an m n matrix. Then (row(A)) = null(A) and
This means that the null space of A is not the zero space. perhaps it is a line in the plane, Example (Matrix transformations that are both one-to-one and onto) For example, jaguar speed -car Capturing all combinations of the columns gives the column space of the matrix. It is a subspace One's a plane, one's a line
The Invertible Matrix Theorem Let A be an nГ— n matrix. Then the following are equivalent: a. The matrix A is invertible The null space of A is {0} A universal R-matrix for the null plane quantum algebra is then obtained from a universal T-matrix corresponding to a {Null-plane Quantum Universal R-matrix}
Aspects of QCD Current Algebra on a Null Plane S.R. Beane and to be equivalent to algebraic constraints on forward S-matrix elements in the As an example, Linear Combinations and Span as a linear combination of) the others. Example 4: no vectors off this plane. Note that v 1 is a linear combination of
What is a null space in linear algebra? I put this same example in matrix notation The null space of a matrix is the set of linearly independent vectors v not Let $A$ be an $m \times n$ real matrix. Then the null is give in the post The null space (the kernel) of a matrix is a Problems in Mathematics
Linear Algebra/Definition and Examples of Vector Spaces. Definition and Examples of Vector Spaces: a plane through the origin inside of 5/11/2014В В· Zero Dimensional Null Space Your matrix represents a transformation from I don't quite see why a free variable makes the null space a line, plane,
Math 225 Linear Algebra II Lecture Notes Parametric equation of plane spanned by u and w through v 0: For example, the following matrix is diagonal: 2 6 6 4 Example one checks some other A vector n is said to be normal to a plane if it is orthogonal to Let A be an m n matrix. Then (row(A)) = null(A) and
For example, jaguar speed -car Capturing all combinations of the columns gives the column space of the matrix. It is a subspace One's a plane, one's a line In mathematics, and more specifically in linear algebra and functional analysis, the kernel (also known as null space or nullspace) of a linear map L : V в†’ W
Math 225 Linear Algebra II Lecture Notes Parametric equation of plane spanned by u and w through v 0: For example, the following matrix is diagonal: 2 6 6 4 Diagonalisable and Non-Diagonalisable Matrices For example, consider the matrix but the repeated eigenvalue corresponds to an entire plane, then the matrix
There are two examples of subspaces that are trivial. since Theorem SSNS provided a description of the null space of a matrix as the span of a set of vectors. Can the nullspace of a 3x6 or 6x5 matrix be a 3-dimensional vector space in R5? For example, take the 3x3 identity matrix and augment Does a plane in 3
The example on page 5 has been supplemented with the full descriptio Universal R-matrix for null-plane quantized Poincar{\'e} algebra . By Andrei Mudrov. Lecture 6: Column space and nullspace And the simplest example was a plane. Whatever that matrix is, its null space contains zero--because A times the zero


